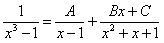01. Considerando que p(x) = 2x³ – kx² + 3x – 2k, para que valores de k temos p(2) = 4?
a) 5
b) -3
c) 3
d) 4
e) 2
02. Determine o valor de a e b no polinômio p(x) = x³ + ax² + (b – 18)x + 1, sabendo que 1 é raiz do polinômio e p(2) = 25. Os valores de a e b são respectivamente:
a) 5 e 4
b) 10 e 6
c) 10 e 5
d) 4 e 10
e) 2 e 8
03. Temos que a raiz do polinômio p(x) = x² – mx + 6 é igual a 6. Calcule o valor de m.
a) 8
b) -7
c) 9
d) 6
e) 7
04.(FEI–SP) Determine A, B e C na decomposição:
a) 1, 2 e 3
b) 1/5, 1/4 e 2
c) 1/2, 2 e 3
d) 1/3, –1/3 e –2/3
e) 1/2, 1/3 e 1
05. (FAAP–SP) Calcule os valores de a, b e c para que o polinômio p(x) = a(x + c)³ + b(x + d) seja idêntico a p(x) = x³ + 6x² + 15x + 14.
a) 1, 2 e 3
b) 2, 1 e 4
c) 1, 3 e 2
d) 1, 5 e 4
e) 1, 2 e 7
06. (MACK – SP) Determine m Є R para que o polinômio p(x) = (m − 4)x³ + (m² – 16)x² + (m + 4)x +4 seja de grau 2.
a) 3
b) 4
c) 1
d) 5
e) Não existe valor para m de modo que o polinômio p(x) seja de grau 2
07. (MACK – SP) Calcule os valores de m, n e l para os quais o polinômio p(x) = (2m – 1)x³ – (5n – 2)x² + (3 – 2l) é nulo.
a) 1/2, 2/5 e 3/2
b) 1/3, 2 e 3
c) 1/2, 2/5 e 3/5
d) 1/2, 2/3 e 3/4
e) 1, 2 e 3
08. (FEI – SP) Sendo p(x) = ax4 + bx³ + c e q(x) = ax³ – bx – c, determine os coeficientes a, b e c, sabendo que p(0) = 0, p(1) = 0 e q(1) = 2.
a) a = 2, b = – 1 e c = 0
b) a = 0, b = – 13 e c = 0
c) a = 1, b = – 1 e c = 0
d) a = 3, b = – 1 e c = 0
e) a = 1, b = – 2 e c = 0
09. Quais são os valores de a e b considerando p(x) = – 4x³ + ax² + bx –18, onde 2 é raiz de p(x) e p(–1) = –18.
a) 8 e 9
b) 10 e 7
c) 6 e 7
d) 8 e 10
e) 7 e 11
RESPOSTAS:
01- C
02- B
03- E
04- D
05- C
06- E
07- A
08- C
09- E